

Next: Preserved under action refinement
Up: Conclusion
Previous: Practical
applications
No abstract semantic equivalence used in concurrency
theory is as easy to decide as branching bisimulation congruence. For
context-free process without silent actions bisimulation equivalence
is the only equivalence in the linear time - branching time spectrum
surveyed in VAN GLABBEEK (1990b) that is
decidable at all (cf. GROOTE & HÜTTEL (1994) and CHRISTENSEN,
HÜTTEL & STIRLING (1995)). For
finite-state processes, (strong) bisimulation equivalence can be
decided in polynomial time, whereas most other equivalences in the
linear time - branching time spectrum are PSPACE-complete (cf.
KANELLAKIS & SMOLKA (1990)).
In GROOTE & VAANDRAGER (1990) an algorithm is
presented for deciding branching bisimulation equivalence between
finite-state processes, with (time) complexity 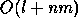 . Here l is
the size of Act, n is the number of nodes in the investigated
process graphs and m the number of edges. The fastest algorithm for
weak bisimulation equivalence up till then had time complexity
. Here l is
the size of Act, n is the number of nodes in the investigated
process graphs and m the number of edges. The fastest algorithm for
weak bisimulation equivalence up till then had time complexity
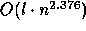 . In general
. In general  , so it
depends on the density of edges in a graph which algorithm is faster.
In a trial implementation of the scheduler of MILNER (1980), reported
in GROOTE & VAANDRAGER (1990), branching bisimulation turned out to
be much faster. Furthermore, it turned out that in such automatic
verifications the space complexity was a much more serious handicap
then the time complexity (the weak bisimulation tools suffered from
lack of memory already when applied to processes with 15.000 states).
The space complexity of the algorithm of GROOTE & VAANDRAGER (1990)
is
, so it
depends on the density of edges in a graph which algorithm is faster.
In a trial implementation of the scheduler of MILNER (1980), reported
in GROOTE & VAANDRAGER (1990), branching bisimulation turned out to
be much faster. Furthermore, it turned out that in such automatic
verifications the space complexity was a much more serious handicap
then the time complexity (the weak bisimulation tools suffered from
lack of memory already when applied to processes with 15.000 states).
The space complexity of the algorithm of GROOTE & VAANDRAGER (1990)
is  , which is less than the space complexity of the weak
bisimulation algorithm. Recently, BOUALI (1992) proposed another
algorithm for weak bisimulation that has the same time complexity as
the branching bisimulation algorithm. An trial with Milner's scheduler
shows that it is somewhat slower, but with a constant factor only. The
space complexity of BOUALI's algorithm is
, which is less than the space complexity of the weak
bisimulation algorithm. Recently, BOUALI (1992) proposed another
algorithm for weak bisimulation that has the same time complexity as
the branching bisimulation algorithm. An trial with Milner's scheduler
shows that it is somewhat slower, but with a constant factor only. The
space complexity of BOUALI's algorithm is 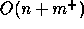 , where
, where 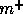 is the
number of edges after taking the t-transitive closure, obtained by
adding an edge p --t-> q whenever there is a nonempty path p ===>
q. This improves the space complexity of the old algorithm for weak
bisimulation, but is not quite as good as the branching bisimulation
algorithm.
is the
number of edges after taking the t-transitive closure, obtained by
adding an edge p --t-> q whenever there is a nonempty path p ===>
q. This improves the space complexity of the old algorithm for weak
bisimulation, but is not quite as good as the branching bisimulation
algorithm.


Next: Preserved under action refinement
Up: Conclusion
Previous: Practical
applications
Rob van Glabbeek
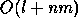 . Here l is
the size of Act, n is the number of nodes in the investigated
process graphs and m the number of edges. The fastest algorithm for
weak bisimulation equivalence up till then had time complexity
. Here l is
the size of Act, n is the number of nodes in the investigated
process graphs and m the number of edges. The fastest algorithm for
weak bisimulation equivalence up till then had time complexity
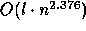 . In general
. In general  , so it
depends on the density of edges in a graph which algorithm is faster.
In a trial implementation of the scheduler of MILNER (1980), reported
in GROOTE & VAANDRAGER (1990), branching bisimulation turned out to
be much faster. Furthermore, it turned out that in such automatic
verifications the space complexity was a much more serious handicap
then the time complexity (the weak bisimulation tools suffered from
lack of memory already when applied to processes with 15.000 states).
The space complexity of the algorithm of GROOTE & VAANDRAGER (1990)
is
, so it
depends on the density of edges in a graph which algorithm is faster.
In a trial implementation of the scheduler of MILNER (1980), reported
in GROOTE & VAANDRAGER (1990), branching bisimulation turned out to
be much faster. Furthermore, it turned out that in such automatic
verifications the space complexity was a much more serious handicap
then the time complexity (the weak bisimulation tools suffered from
lack of memory already when applied to processes with 15.000 states).
The space complexity of the algorithm of GROOTE & VAANDRAGER (1990)
is  , which is less than the space complexity of the weak
bisimulation algorithm. Recently, BOUALI (1992) proposed another
algorithm for weak bisimulation that has the same time complexity as
the branching bisimulation algorithm. An trial with Milner's scheduler
shows that it is somewhat slower, but with a constant factor only. The
space complexity of BOUALI's algorithm is
, which is less than the space complexity of the weak
bisimulation algorithm. Recently, BOUALI (1992) proposed another
algorithm for weak bisimulation that has the same time complexity as
the branching bisimulation algorithm. An trial with Milner's scheduler
shows that it is somewhat slower, but with a constant factor only. The
space complexity of BOUALI's algorithm is 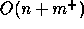 , where
, where 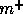 is the
number of edges after taking the t-transitive closure, obtained by
adding an edge p --t-> q whenever there is a nonempty path p ===>
q. This improves the space complexity of the old algorithm for weak
bisimulation, but is not quite as good as the branching bisimulation
algorithm.
is the
number of edges after taking the t-transitive closure, obtained by
adding an edge p --t-> q whenever there is a nonempty path p ===>
q. This improves the space complexity of the old algorithm for weak
bisimulation, but is not quite as good as the branching bisimulation
algorithm.