All *-bisimulations (*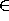 
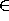w,b,eta,d) have relatively
simple equational characterizations (see Section 2). However, the
listed axioms are in no way self-evident, but arise from the semantic
presentation of the respective notions. In the presence of the
(plausible) axioms of strong equivalence, branching bisimulation
congruence on finite closed terms is completely axiomatized by the
(equally plausible) first t-law (atx=ax) alone
(VAN GLABBEEK (1993a)). This means that
the algebra of branching bisimulation can be understood without
appealing to semantic notions at all.