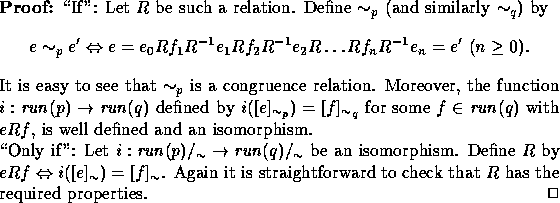 be a class of processes. I assume that for each process
be a class of processes. I assume that for each process
 a set
a set  of (partial) runs is defined, equipped
with a prefix ordering
of (partial) runs is defined, equipped
with a prefix ordering  , and that with each run (or
execution)
, and that with each run (or
execution) 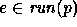 is associated its observable content
is associated its observable content 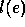 .
.
Let 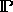 be a class of processes. I assume that for each process
be a class of processes. I assume that for each process
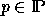 a set
a set 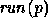 of (partial) runs is defined, equipped
with a prefix ordering
of (partial) runs is defined, equipped
with a prefix ordering  , and that with each run (or
execution)
, and that with each run (or
execution) 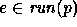 is associated its observable content
is associated its observable content 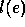 .
.
A first idea of what could be the branching structure of a process 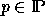 , is the pomset with representative
, is the pomset with representative 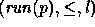 . This I
will call the strict branching structure of p, as it
corresponds with the idea that the branching of all, possibly
indistinguishable, runs is taken into account. In order to
arrive at a less strict definition, one needs to identify certain
runs.
. This I
will call the strict branching structure of p, as it
corresponds with the idea that the branching of all, possibly
indistinguishable, runs is taken into account. In order to
arrive at a less strict definition, one needs to identify certain
runs.
This is the intermediate variant of three possible generalizations of
the concept of a congruence from algebras to algebraic structures with
relations. A strong congruence would even require that 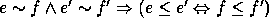 , so
that
, so
that 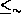 can simply be defined by
can simply be defined by 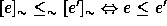 . A weak congruence
on the other hand doesn't require anything for
. A weak congruence
on the other hand doesn't require anything for  , and
, and
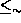 needs to be defined by
needs to be defined by 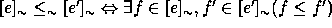 .
.
Obviously a coarsest congruence on a pomset exists, as the union of arbitrary many congruences is again a congruence. The following observations are meant as tool for deciding whether or not a model or equivalence respects branching time.
Proof: This follows immediately from the following two facts, whose proofs are straightforward.
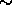 is the coarsest and
is the coarsest and 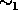 any congruence on an
elpo
any congruence on an
elpo 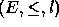 , and
, and 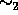 is the coarsest congruence on
is the coarsest congruence on
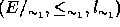 , then
, then
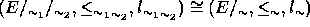 .
.
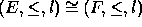 and
and 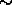 is a congruence on
is a congruence on
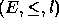 , then there is a congruence
, then there is a congruence 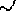 on
on 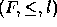 such
that
such
that 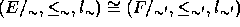 . Moreover,
. Moreover, 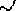 is the
coarsest iff
is the
coarsest iff 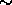 is.
is.