Sorav Bansal
Computer Systems Lab
Stanford University
Alex Aiken
Computer Systems Lab
Stanford University
A common worry for machine architects is how to run existing software on new architectures. One way to deal with the problem of software portability is through binary translation. Binary translation enables code written for a source architecture (or instruction set) to run on another destination architecture, without access to the original source code. A good example of the application of binary translation to solve a pressing software portability problem is Apple's Rosetta, which enabled Apple to (almost) transparently move its existing software for the Power-based Macs to a new generation of Intel x86-based computers [1].
Building a good binary translator is not easy, and few good binary translation tools exist today. There are four main difficulties:
Our work presents a new approach to addressing problems (1)-(3) (we do not address problem (4)). The main idea is that much of the complexity of writing an aggressively optimizing translator between two instruction sets can be eliminated altogether by developing a system that automatically and systematically learns translations. In Section 6 we present performance results showing that this approach is capable of producing destination machine code that is at least competitive with existing state-of-the-art binary translators, addressing problem (1). While we cannot meaningfully compare the engineering effort needed to develop our research project with what goes into commercial tools, we hope to convince the reader that, on its face, automatically learning translations must require far less effort than hand coding translations between architectures, addressing problem (2). Similarly, we believe our approach helps resolve the tension between performance and retargetability: adding a new architecture requires only a parser for the binary format and a description of the instruction set semantics (see Section 3). This is the minimum that any binary translator would require to incorporate a new architecture; in particular, our approach has no intermediate language that must be expanded or tweaked to accommodate the unique features of an additional architecture.
Our system uses peephole rules to translate code from one architecture to another. Peephole rules are pattern matching rules that replace one sequence of instructions by another equivalent sequence of instructions. Peephole rules have traditionally been used for compiler-optimizations, where the rules are used to replace a sub-optimal instruction sequence in the code by another equivalent, but faster, sequence. For our binary translator, we use peephole rules that replace a source-architecture instruction sequence by an equivalent destination architecture instruction sequence. For example,
ld [r2]; addi 1; st [r2] =>
inc [er3] { r2 = er3 }
is a peephole translation rule from a certain accumulator-based RISC
architecture to another CISC architecture. In this case, the rule expresses
that the operation of loading
a value from memory location [r2], adding 1 to it and storing it
back to [r2] on the RISC machine can be achieved by a single
in-memory increment instruction on location [er3] on the CISC machine,
where RISC register r2 is emulated by CISC register er3.
The number of peephole rules required to correctly translate a complete executable for any source-destination architecture pair can be huge and manually impossible to write. We automatically learn peephole translation rules using superoptimization techniques: essentially, we exhaustively enumerate possible rules and use formal verification techniques to decide whether a candidate rule is a correct translation or not. This process is slow; in our experiments it required about a processor-week to learn enough rules to translate full applications. However, the search for translation rules is only done once, off-line, to construct a binary translator; once discovered, peephole rules are applied to any program using simple pattern matching, as in a standard peephole optimizer. Superoptimization has been previously used in compiler optimization [5,10,14], but our work is the first to develop superoptimization techniques for binary translation.
Binary translation preserves execution semantics on two different machines: whatever result is computed on one machine should be computed on the other. More precisely, if the source and destination machines begin in equivalent states and execute the original and translated programs respectively, then they should end in equivalent states. Here, equivalent states implies we have a mapping telling us how the states of the two machines are related. In particular, we must decide which registers/memory locations on the destination machine emulate which registers/memory locations of the source machine.
Note that the example peephole translation rule given above is conditioned by the register map r2 = er3. Only when we have decided on a register map can we compute possible translations. The choice of register map turns out to be a key technical problem: better decisions about the register map (e.g., different choices of destination machine registers to emulate source machine registers) lead to better performing translations. Of course, the choice of instructions to use in the translation also affects the best choice of register map (by, for example, using more or fewer registers), so the two problems are mutually recursive. We present an effective dynamic programming technique that finds the best register map and translation for a given region of code (Section 3.3).
We have implemented a prototype binary translator from PowerPC to x86. Our prototype handles nearly all of the PowerPC and x86 opcodes and using it we have successfully translated large executables and libraries. We report experimental results on a number of small compute-intensive microbenchmarks, where our translator surprisingly often outperforms the native compiler. We also report results on many of the SPEC integer benchmarks, where the translator achieves a median performance of around 67% of natively compiled code and compares favorably with both Qemu [17], an open source binary translator, and Apple's Rosetta [1]. While we believe these results show the usefulness of using superoptimization as a binary translation and optimization tool, there are two caveats to our experiments that we discuss in more detail in Section 6. First, we have not implemented translations of all system calls. As discussed above under problem (4), this is a separate and quite significant engineering issue. We do not believe there is any systematic bias in our results as a result of implementing only enough system calls to run many, but not all, of the SPEC integer benchmarks. Second, our system is currently a static binary translator, while the systems we compare to are dynamic binary translators, which may give our system an advantage in our experiments as time spent in translation is not counted as part of the execution time. There is nothing that prevents our techniques from being used in a dynamic translator; a static translator was just easier to develop given our initial tool base. We give a detailed analysis of translation time, which allows us to bound the additional cost that would be incurred in a dynamic translator.
In summary, our aim in this work is to demonstrate the ability to develop binary translators with competitive performance at much lower cost. Towards this end, we make the following contributions:
The rest of this paper is organized as follows. We begin with a discussion on the recent applications of binary translation (Section 2). We then provide a brief overview of peephole superoptimizers followed by a discussion on how we employ them for binary translation (Section 3). We discuss other relevant issues involved in binary translation (Section 4) and go on to discuss our prototype implementation (Section 5). We then present our experimental results (Section 6), discuss related work (Section 7), and finally conclude (Section 8).
Before describing our binary translation system, we give a brief overview of a range of applications for binary translation. Traditionally, binary translation has been used to emulate legacy architectures on recent machines. With improved performance, it is now also seen as an acceptable portability solution.
Binary translation is useful to hardware designers for ensuring software availability for their new architectures. While the design and production of new architecture chips complete within a few years, it can take a long time for software to be available on the new machines. To deal with this situation and ensure early adoption of their new designs, computer architects often turn to software solutions like virtual machines and binary translation [7].
Another interesting application of binary translation for hardware vendors is backward and forward compatibility of their architecture generations. To run software written for older generations, newer generations are forced to support backward compatibility. On the flip side, it is often not possible to run newer generation software on older machines. Both of these problems create compatibility headaches for computer architects and huge management overheads for software developers. It is not hard to imagine the use of a good binary-translation based solution to solve both problems in the future.
Binary translation is also being used for machine and application virtualization. Leading virtualization companies are now considering support for allowing the execution of virtual machines from multiple architectures on a single host architecture [20]. Hardware vendors are also developing virtualization platforms that allow people to run popular applications written for other architectures on their machines [16]. Server farms and data centers can use binary translation to consolidate their servers, thus cutting their power and management costs.
People have also used binary translation to improve performance and reduce power consumption in hardware. Transmeta Crusoe [12] employs on-the-fly binary translation to execute x86 instructions on a VLIW architecture thereby cutting power costs [11]. Similarly, in software, many Java virtual machines perform on-the-fly translation from Java bytecode to the host machine instructions [25] to improve execution performance.
In this section we give a necessarily brief overview of the design and functionality of peephole superoptimizers, focusing on the aspects that are important in the adaptation to binary translation.
Once constructed, the optimizer is applied to an executable by simply looking up target sequences in the executable for a known better replacement. The purpose of using harvested instruction sequences is to focus the search for optimizations on the code sequences (usually generated by other compilers) that appear in actual programs. Typically, all instruction sequences up to length 5 or 6 are harvested, and the enumerator tries all instruction sequences up to length 3 or 4. Even at these lengths, there are billions of enumerated instruction sequences to consider, and techniques for pruning the search space are very important [5]. Thus, the construction of the peephole optimizer is time-consuming, requiring a few processor-days. In contrast, actually applying the peephole optimizations to a program typically completes within a few seconds.
The enumerator's equivalence test is performed in two stages: a fast execution test and a slower boolean test. The execution test is implemented by executing the target sequence and the enumerated sequence on hardware and comparing their outputs on random inputs. If the execution test does not prove that the two sequences are different (i.e., because they produce different outputs on some tested input), the boolean test is used. The equivalence of the two instruction sequences is expressed as boolean formula: each bit of machine state touched by either sequence is encoded as a boolean variable, and the semantics of instructions is encoded using standard logical connectives. A SAT solver is then used to test the formula for satisfiability, which decides whether the two sequences are equal.
|
Using these techniques, all length-3 x86 instruction sequences have previously been enumerated on a single processor in less than two days [5]. This particular superoptimizer is capable of handling opcodes involving flag operations, memory accesses and branches, which on most architectures covers almost all opcodes. Equivalence of instruction sequences involving memory accesses is correctly computed by accounting for the possibility of aliasing. The optimizer also takes into account live register information, allowing it to find many more optimizations because correctness only requires that optimizations preserve live registers (note the live register information qualifying the peephole rules in Table 1).
The binary translator's harvester first extracts target sequences from a training set of source-architecture applications. The enumerator then enumerates instruction sequences on the destination architecture checking them for equivalence with any of the target sequences. A key issue is that the definition of equivalence must change in this new setting with different machine architectures. Now, equivalence is meaningful only with respect to a register map showing which memory locations on the destination machine, and in particular registers, emulate which memory locations on the source machine; some register maps are shown in Table 2. A register in the source architecture could be mapped to a register or a memory location in the destination architecture. It is also possible for a memory location in the source architecture to be mapped to a register in the destination architecture.
|
A potential problem is that for a given source-architecture instruction sequence there may be many valid register maps, yielding a large number of (renamed) instruction sequences on the target-architecture that must be tested for equivalence. For example, the two registers used by the PowerPC register move instruction mr r1,r2 can be mapped to the 8 registers of the x86 in 8*7=56 different ways. Similarly, there may be many variants of a source-architecture instruction sequence. For example, on the 32 register PowerPC, there are 32*31=992 variants of mr r1, r2. We avoid these problems by eliminating source-architecture sequences that are register renamings of one canonically-named sequence and by considering only one register map for all register maps that are register renamings of each other. During translation, a target sequence is (canonically) renamed before searching for a match in the peephole table and the resulting translated sequence is renamed back before writing it out. Further details of this canonicalization optimization are in [5].
When an enumerated sequence is found to be equivalent to a target sequence, the corresponding peephole rule is added to the translation table together with the register map under which the translation is valid. Some examples of peephole translation rules are shown in Table 3.
Once the binary translator is constructed, using it is relatively simple. The translation rules are applied to the source-architecture code to obtain destination-architecture code. The application of translation rules is more involved than the application of optimization rules. Now, we also need to select the register map for each code point before generating the corresponding translated code. The choice of register map can make a noticeable difference to the performance of generated code. We discuss the selection of optimal register maps at translation time in the next section.
|
We formulate a dynamic programming problem to choose a minimum cost register map
at each program point in a given code region.
At each code point, we enumerate all register maps that are likely to
produce a translation.
Because the space of all register maps is huge, it is important to constrain
this space by identifying only the relevant register maps.
We consider the register maps
at all predecessor code points and extend them using
the registers used by the current target sequence. For each register used
by the current target sequence, all possibilities
of register mappings (after discarding register renamings) are
enumerated.
Also, we attempt to avoid enumerating register maps that will produce
an identical translation
to a register map that has already been enumerated, at an equal or higher cost.
For each enumerated register map ![]() , the peephole translation
table is queried for a matching translation rule
, the peephole translation
table is queried for a matching translation rule ![]() and the corresponding
translation cost is recorded.
We consider length-
and the corresponding
translation cost is recorded.
We consider length-![]() to length-
to length-![]() instruction sequences while querying the
peephole table for each enumerated register map. Note that there may
be multiple possible translations at a given code point, just as there may
be multiple valid register maps; we simply keep track of all possibilities.
The dynamic programming
problem formulation then considers the translation produced for each
sequence length while determining the optimal translation for a block of code.
Assume for simplicity that the code point under consideration has only one
predecessor,
and the possible register maps at the predecessor are
instruction sequences while querying the
peephole table for each enumerated register map. Note that there may
be multiple possible translations at a given code point, just as there may
be multiple valid register maps; we simply keep track of all possibilities.
The dynamic programming
problem formulation then considers the translation produced for each
sequence length while determining the optimal translation for a block of code.
Assume for simplicity that the code point under consideration has only one
predecessor,
and the possible register maps at the predecessor are
![]() .
For simplicity, we also assume that we are translating one instruction at a time
and that
.
For simplicity, we also assume that we are translating one instruction at a time
and that ![]() is the minimum cost translation for that instruction if register
map
is the minimum cost translation for that instruction if register
map ![]() is used.
The best cost register map
is used.
The best cost register map ![]() is then the one that minimizes the cost of switching
from a predecessor map
is then the one that minimizes the cost of switching
from a predecessor map ![]() to
to ![]() , the cost of the instruction sequence
, the cost of the instruction sequence ![]() ,
and, recursively, the cost of
,
and, recursively, the cost of ![]() :
:
To translate multiple source-architecture instructions using a single
peephole rule, we extend this approach
to consider translations for all length-![]() to length-
to length-![]() sequences that end
at the current code point. For example, at the end of instruction
sequences that end
at the current code point. For example, at the end of instruction ![]() in
an instruction sequence
in
an instruction sequence
![]() , we search for possible
translations for
each of the sequences
, we search for possible
translations for
each of the sequences ![]() ,
, ![]() and
and
![]() to find the lowest-cost translation.
While
considering a translation for the sequence
to find the lowest-cost translation.
While
considering a translation for the sequence
![]() , the predecessor
register maps considered are the register maps at instruction
, the predecessor
register maps considered are the register maps at instruction ![]() .
Similarly, the predecessor register maps for sequences
.
Similarly, the predecessor register maps for sequences ![]() and
and
![]() are maps at instructions
are maps at instructions ![]() and
and ![]() respectively.
The cost of register map
respectively.
The cost of register map ![]() is then the minimum among the costs computed
for each sequence length.
is then the minimum among the costs computed
for each sequence length.
We solve the recurrence in a standard fashion. Beginning at start of a code region (e.g., a function body), the cost of the preceding register map is initially 0. Working forwards through the code region, the cost of each enumerated register map is computed and stored before moving to the next program point and repeating the computation. When the end of the code region is reached, the register map with the lowest cost is chosen and its decisions are backtracked to decide the register maps and translations at all preceding program points. For program points having multiple predecessors, we use a weighted sum of the switching costs from each predecessor. To handle loops, we perform two iterations of this computation. Interesting examples are too lengthy to include here, but a detailed, worked example of register map selection is in [4].
This procedure of enumerating all register maps and then
solving a dynamic programming problem is computationally intensive
and, if not done properly, can significantly increase translation time.
While
the cost of finding the best register map for every code point is not a problem for a
static translator, it would add significant overhead to a dynamic translator.
To bound the computation time, we prune the set of enumerated register
maps at each program point. We retain only the ![]() lowest-cost
register maps before moving to the next program point. We allow the value of
lowest-cost
register maps before moving to the next program point. We allow the value of
![]() to be tunable and refer to it as the prune size.
We also have the flexibility to trade
computation
time for lower quality solutions. For example, for code that is not
performance critical
we can consider code regions of size one (e.g., a single instruction) or even
use
a fixed register map. In Section 6 we show that the cost
of computing
the best register maps for frequently executed instructions is very small
for our benchmarks.
We also discuss the performance sensitivity of our benchmarks to the
prune size.
to be tunable and refer to it as the prune size.
We also have the flexibility to trade
computation
time for lower quality solutions. For example, for code that is not
performance critical
we can consider code regions of size one (e.g., a single instruction) or even
use
a fixed register map. In Section 6 we show that the cost
of computing
the best register maps for frequently executed instructions is very small
for our benchmarks.
We also discuss the performance sensitivity of our benchmarks to the
prune size.
Our binary translator is static, though we have avoided including anything in our implementation that would make it impractical to develop a dynamic translator (e.g., whole-program analysis or optimizations) using the same algorithms. Most of the techniques we discuss are equally applicable in both settings and, when they are not, we discuss the two separately.
While dealing with source-destination architecture pairs with different endianness, special care is required in handling OS-related data structures. In particular, all executable headers, environment variables and program arguments in the program's address space need to be converted from destination endianness to source endianness before transferring control to the translated program. This step is necessary because the source program assumes source endianness for everything while the OS writes the data structures believing that the program assumes destination endianness. In a dynamic translator, these conversions are performed inside the translator at startup. In a static translator, special initialization code is emitted to perform these conversions at runtime.
To handle conditional jumps, the condition codes of the source architecture need to be faithfully represented in the destination architecture. Handling condition codes correctly is one of the more involved aspects of binary translation because of the divergent condition-code representations used by different architectures. We discuss our approach to handling condition codes in the context of our PowerPC-x86 binary translator; see Section 5.3. The handling of indirect jumps is more involved and is done differently for static and dynamic translators. We discuss this in detail in Section 5.4.
The translator has been implemented in C/C++ and O'Caml [13]. Our superoptimizer is capable of automatically inferring peephole translation rules from PowerPC to x86. Because we cannot execute both the target sequence and the enumerated sequence on the same machine, we use a PowerPC emulator (we use Qemu in our experiments) to execute the target sequence. Recall from Section 3.1 that there are two steps to determining which, if any, target instruction sequences are equivalent to the enumerated instruction sequence: first a fast execution test is used to eliminate all but few plausible candidates, and then a complete equivalence check is done by converting both instruction sequences to boolean formulas and deciding a satisfiability query. We use zChaff [15,26] as our backend SAT solver. We have translated most, but not all, Linux PowerPC system calls. We present our results using a static translator that produces an x86 ELF 32-bit binary executable from a PowerPC ELF 32-bit binary. Because we used the static peephole superoptimizer described in [5] as our starting point, our binary translator is also static, though as discussed previously our techniques could also be applied in a dynamic translator. A consequence of our current implementation is that we also translate all the shared libraries used by the PowerPC program.
In this section, we discuss issues specific to a PowerPC-x86 binary translator. While there exist many architecture-specific issues (as we discuss in this section), the vast bulk of the translation and optimization complexity is still hidden by the superoptimizer.
While PowerPC condition codes are written using separate instructions, x86 condition codes are overwritten by almost all x86 instructions. Moreover, while PowerPC compare instructions explicitly state whether they are doing a signed or an unsigned comparison and store only one result in their flags, x86 compare instructions perform both signed and unsigned comparisons and store both results in their condition bits. On x86, the branch instruction then specifies which comparison it is interested in (signed or unsigned).
 |
 |
Handling an indirect jump in a dynamic translator is simpler. Here, on encountering an indirect jump, we relinquish control to the translator. The translator then performs the register map conversion before transferring control to the (translated) destination address.
Handling an indirect jump in a static translator is more involved. We first identify all instructions that can be possible indirect jump targets. Since almost all well-formed executables use indirect jumps in only a few different code paradigms, it is possible to identify possible indirect jump targets by scanning the executable. We scan the read-only data sections, global offset tables and instruction immediate operands and use a set of pattern matching rules to identify possible indirect jump targets. A lookup table is then constructed to map these jump targets (which are source architecture addresses) to their corresponding destination architecture addresses. However, as we need to perform register map conversion before jumping to the destination address at runtime, we replace the destination addresses in the lookup table with the address of a code fragment that performs the register-map conversion before jumping to the destination address.
The translation of an indirect jump involves a table lookup and some register-map conversion code. While the table lookup is fast, the register-map conversion may involve multiple memory accesses. Hence, an indirect jump is usually an expensive operation.
Although the pattern matching rules we use to identify possible indirect jump targets have worked extremely well in practice, they are heuristics and are prone to adversarial attacks. It would not be difficult to construct an executable that exploits these rules to cause a valid PowerPC program to crash on x86. Hence, in an adversarial scenario, it would be wise to assume that all code addresses are possible indirect jump targets. Doing so results in a larger lookup table and more conversion code fragments, increasing the overall size of the executable, but will have no effect on running time apart from possible cache effects.
|
We implement function calls of the PowerPC architecture by simply emulating the link-register (lr) like any other PowerPC register. On a function call (bl), the link register is updated with the value of the next PowerPC instruction pointer. A function return (blr) is treated just like an indirect jump to the link register.
The biggest advantage of using this scheme is its simplicity. However, it is possible to improve the translation of the blr instruction by exploiting the fact that blr is always used to return from a function. For this reason, it is straightforward to predict the possible jump targets of blr at translation time (it will be the instruction following the function call bl). At runtime, the value of the link register can then be compared to the predicted value to see if it matches, and then jump accordingly. This information can be used to avoid the extra memory reads and writes required for register map conversion in an indirect jump. We have implemented this optimization; while this optimization provides significant improvements while translating small recursive benchmarks (e.g., recursive computation of the fibonacci series), it is not very effective for larger benchmarks (e.g., SPEC CINT2000).
|
To be able to generate peephole translations involving these special instructions, the superoptimizer is made aware of the constraints on their operands during enumeration. If a translation is found by the superoptimizer involving these special instructions, the generated peephole rule encodes the name constraints on the operands as register name constraints. These constraints are then used by the translator at code generation time.
|
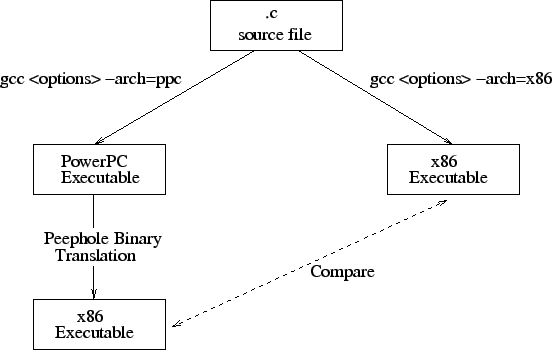 |
In our experiments, we compare the executable produced by our
translator to a natively-compiled
executable. The experimental setup is shown in Figure 3.
We compile from the C source for both PowerPC and x86 platforms using gcc.
The same compiler optimization options are used for both platforms. The
PowerPC executable is then translated using our binary
translator to an x86 executable. And finally, the translated x86 executable
is compared with the natively-compiled one for performance.
|
One would expect the performance of the translated executable to be strictly lower than that of the natively-compiled executable. To get an idea of the state-of-the-art in binary translation, we discuss two existing binary translators. A general-purpose open-source emulator, Qemu [17], provides 10-20% of the performance of a natively-compiled executable (i.e., 5-10x slowdown). A recent commercially available tool by Transitive Corporation [22] (which is also the basis of Apple's Rosetta translator) claims ``typically about 70-80%'' of the performance of a natively-compiled executable on their website [18]. Both Qemu and Transitive are dynamic binary translators, and hence Qemu and Rosetta results include the translation overhead, while the results for our static translator do not. We estimate the translation overhead of our translator in Section 6.1.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
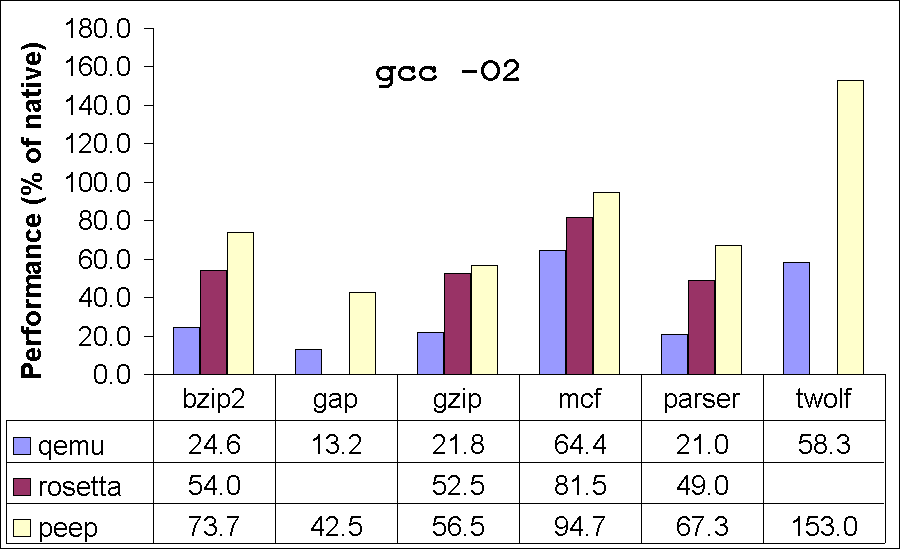 |
Table 7 shows the performance of our binary translator on small compute-intensive microbenchmarks. (All reported runtimes are computed after running the executables at least 3 times.) Our microbenchmarks use three well-known sorting algorithms, three different algorithms to solve the Towers of Hanoi, one benchmark that computes the Fibonacci sequence, a link-list traversal, a binary search on a sorted array, and an empty for-loop. All these programs are written in C. They are all highly compute-intensive and hence designed to stress-test the performance of binary translation.
The translated executables perform roughly at 90% of the performance of a natively-compiled executable on average. Some benchmarks perform as low as 64% of native performance and many benchmarks outperform the natively compiled executable. The latter result is a bit surprising. For unoptimized executables, the binary translator often outperforms the natively compiled executable because the superoptimizer performs optimizations that are not seen in an unoptimized natively compiled executable. The bigger surprise occurs when the translated executable outperforms an already optimized executable (columns -O2 and -O2ofp) indicating that even mature optimizing compilers today are not producing the best possible code. Our translator sometimes outperforms the native compiler for two reasons:
A striking result is the performance of the fibo benchmark in the -O2 column where the translated executable is almost three times faster than the natively-compiled and optimized executable. On closer inspection, we found that this is because gcc, on x86, uses one dedicated register to store the frame pointer by default. Since the binary translator makes no such reservation for the frame pointer, it effectively has one extra register. In the case of fibo, the extra register avoids a memory spill present in the natively compiled code causing the huge performance difference. Hence, for a more equal comparison, we also compare with the `-fomit-frame-pointer' gcc option on x86 (-O2ofp column).
Table 8 gives the results for seven of the SPEC integer benchmarks. (The other benchmarks failed to run correctly due to the lack of complete support for all Linux system calls in our translator). Figure 4 compares the performance of our translator to Qemu and Rosetta. In our comparisons with Qemu, we used the same PowerPC and x86 executables as used for our own translator. For comparisons with Rosetta, we could not use the same executables, as Rosetta supports only Mac executables while our translator supports only Linux executables. Therefore, to compare, we recompiled the benchmarks on Mac to measure Rosetta performance. We used exactly the same compiler version (gcc 4.0.1) on the two platforms (Mac and Linux). We ran our Rosetta experiments on a Mac Mini Intel Core 2 Duo 1.83GHz processor, 32KB L1-Icache, 32KB L1-Dcache, 2MB L2-cache and 2GB of memory. These benchmarks spend very little time in the kernel, and hence we do not expect any bias in results due to differences in the two operating systems. The differences in the hardware could cause some bias in the performance comparisons of the two translators. While it is hard to predict the direction and magnitude of this bias, we expect it to be insignificant.
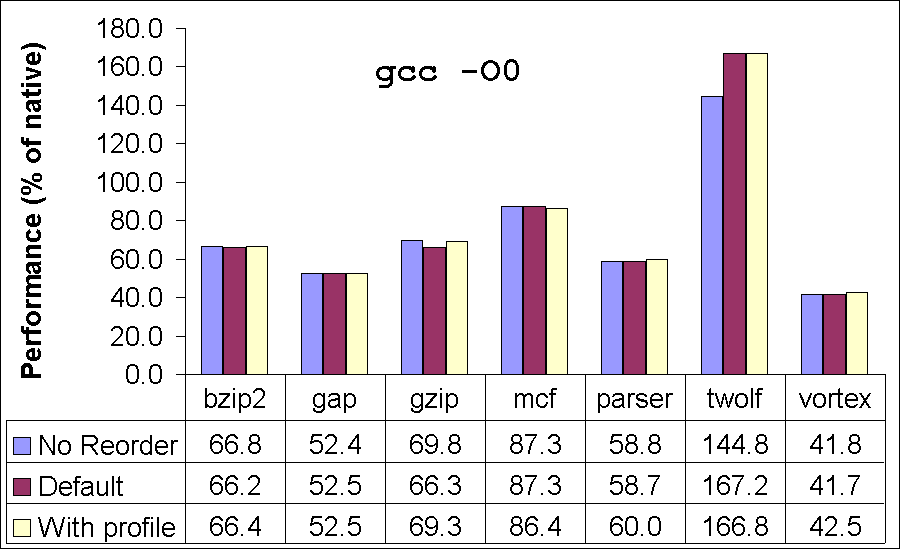
Our peephole translator fails on vortex when it is compiled using -O2. Similarly, Rosetta fails on twolf for both optimization options. These failures are most likely due to bugs in the translators. We could not obtain performance numbers for Rosetta on gap because we could not successfully build gap on Mac OS X. Our peephole translator achieves a performance of 42-164% of the natively compiled executable. Comparing with Qemu, our translator achieves 1.3-4x improvement in performance. When compared with Apple Rosetta, our translator performs 12% better (average) on the executables compiled with -O2 and 3% better on the executables compiled with -O0. Our system performs as well or better than Rosetta on almost all our benchmarks, the only exceptions being -O0 for vortex where the peephole translator produces code 1.4% slower than Rosetta, and -O2 for vortex, which the peephole translator fails to translate. The median performance of the translator on these compute-intensive benchmarks is 67% of native code.
 |
 |
Next, we consider the performance of our translator on SPEC benchmarks by toggling some of the optimizations. The purpose of these experiments is to obtain insight into the performance impact of these optimizations. We consider two variants of our translator:
Our superoptimizer uses a peephole size of at most 2 PowerPC instructions. The x86 instruction sequence in a peephole rule can be larger and is typically 1-3 instructions long. Each peephole rule is associated with a cost that captures the approximate cycle cost of the x86 instruction sequence.
We compute the peephole table offline only once for every source-destination architecture pair. The computation of the peephole table can take up to a week on a single processor. On the other hand, applying the peephole table to translate an executable is fast (see Section 6.1). For these experiments, the peephole table consisted of approximately 750 translation rules. Given more time and resources, it is straightforward to scale the number of peephole rules by running the superoptimizer on longer length sequences. More peephole rules are likely to give better performance results.
The size of the translated executable is roughly 5-6x larger than the
source PowerPC executable.
Of the total size of the translated executable,
roughly 40% is occupied by
the translated code, 20% by the code and data sections of the original
executable, 25% by the indirect jump lookup table and the remaining 15%
by other management code and data.
For our benchmarks, the average size of the code sections in the original
PowerPC executables is around 650 kilobytes, while the average size of the
code sections in the translated executables is around 1400 kilobytes.
Because both the original and translated executables operate on the same
data and these benchmarks spend more than ![]() of their time in less
than
of their time in less
than ![]() of the code, we expect their working set sizes to be roughly the same.
of the code, we expect their working set sizes to be roughly the same.
Our static translator takes 2-6 minutes to translate an executable with around 100K instructions, which includes the time to disassemble a PowerPC executable, compute register liveness information for each function, perform the actual translation including computing the register map for each program point (see Section 3.3), build the indirect jump table and then write the translated executable back to disk. Of these various phases, computing the translation and register maps accounts for the vast majority of time.
A dynamic translator, on the other hand, typically translates instructions when, and only when, they are executed. Thus, no time is spent translating instructions that are never executed. Because most applications use only a small portion of their extensive underlying libraries, in practice dynamic translators only translate a small part of the program. Moreover, dynamic translators often trade translation time for code quality, spending more translation time and generating better code for hot code regions.
To understand the execution characteristics of a typical executable, we
study our translator's performance on bzip2 in detail. (Because
all of our applications build on the same standard libraries, which form
the overwhelming majority of the code, the behavior of the other applications
is similar to bzip2.)
Of the 100K instructions in bzip2, only around
8-10K instructions are ever executed in the benchmark runs. Of these, only
around 2K instructions (hot regions) account for more than ![]() of the
execution time.
Figure 6 shows the time spent in translating the
hot regions of code using our translator.
of the
execution time.
Figure 6 shows the time spent in translating the
hot regions of code using our translator.
We plot the translation time with varying prune
sizes; because computing the translation and register maps dominate,
the most effective way for our system to trade code quality for
translation speed is by adjusting the prune size (recall Section 3.3).
We also plot the performance
of the translated executable at these prune sizes. At prune size 0
, an
arbitrary
register map is chosen where all PowerPC registers are mapped to memory.
At this point, the translation time of the hot regions is very
small (less than ![]() seconds) at the cost of the execution time of
the translated executable.
At prune size
seconds) at the cost of the execution time of
the translated executable.
At prune size ![]() however, the translation time increases to
however, the translation time increases to ![]() seconds
and the performance already reaches 74% of native.
At higher prune sizes, the translation
overhead increases significantly with only a small improvement in runtime
(for bzip2, the runtime improvement is 2%).
This indicates that even at a small prune
size (and hence a low translation time), we
obtain good performance.
While higher prune sizes do not significantly improve the performance of the
translator on SPEC benchmarks, they make a significant difference to the
performance of tight inner loops in some of our microbenchmarks.
seconds
and the performance already reaches 74% of native.
At higher prune sizes, the translation
overhead increases significantly with only a small improvement in runtime
(for bzip2, the runtime improvement is 2%).
This indicates that even at a small prune
size (and hence a low translation time), we
obtain good performance.
While higher prune sizes do not significantly improve the performance of the
translator on SPEC benchmarks, they make a significant difference to the
performance of tight inner loops in some of our microbenchmarks.
Finally, we point out that while the translation cost reported in Figure 6 accounts for only the translation of hot code regions, we can use a fast and naive translation for the cold regions. In particular, we can use an arbitrary register map (prune size of 0 ) for the rarely executed instructions to produce fast translations of the remaining code; for bzip2 it takes less than 1 second to translate the cold regions using this approach. Thus we estimate that a dynamic translator based on our techniques would require under 10 seconds in total to translate bzip2, or less than 4% of the 265 seconds of run-time reported in Table 8.
By the mid-1990's more binary translators had appeared: IBM's DAISY [8] used hardware support to translate popular architectures to VLIW architectures, Digital's FX!32 ran x86/WinNT applications on Alpha/WinNT [7], Ardi's Executor [9] ran old Macintosh applications on PCs, Sun's Wabi [21] executed Microsoft Windows applications in UNIX environments and Embra [24], a machine simulator, simulated the processors, caches and other memory systems of uniprocessors and cache-coherent multiprocessors using binary translation. A common feature in all these tools is that they were all designed to solve a specific problem and were tightly coupled to the source and/or destination architectures and operating systems. For this reason, no meaningful performance comparisons exist among these tools.
More recently, the moral equivalent of binary translation is used extensively in Java just-in-time (JIT) compilers to translate Java bytecode to the host machine instructions. This approach is seen as an efficient solution to deal with the problem of portability. In fact, some recent architectures especially cater to Java applications as these applications are likely to be their first adopters [2].
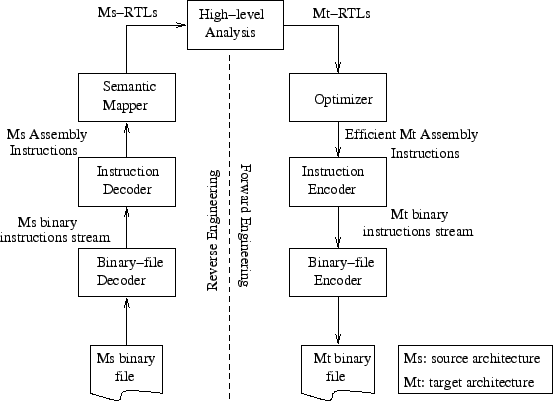
An early attempt to build a general purpose binary translator was the UQBT framework [23] that described the design of a machine-adaptable dynamic binary translator. The design of the UQBT framework is shown in Figure 7. The translator works by first decoding the machine-specific binary instructions to a higher level RTL-like language (RTL stands for register transfer lists). The RTLs are optimized using a machine-independent optimizer, and finally machine code is generated for the destination architecture from the RTLs. Using this approach, UQBT had up to a 6x slowdown in their first implementation. A similar approach has been taken by a commercial tool being developed at Transitive Corporation [22]. Transitive first disassembles and decodes the source instructions to an intermediate language, performs optimizations on the intermediate code and finally assembles it back to the destination architecture. In their current offerings, Transitive supports SPARC-x86, PowerPC-x86, SPARC-x86/64-bit and SPARC-Itanium source-destination architecture pairs.
 |
A potential weakness in the approach used by UQBT and Transitive is the reliance on a well-designed intermediate RTL language. A universal RTL language would need to capture the peculiarities of all different machine architectures. Moreover, the optimizer would need to understand these different language features and be able to exploit them. It is a daunting task to first design a good and universal intermediate language and then write an optimizer for it, and we believe using a single intermediate language is hard to scale beyond a few architectures. Our comparisons with Apple Rosetta (Transitive's PowerPC-x86 binary translator) suggest that superoptimization is a viable alternative and likely to be easier to scale to many machine pairs.
In recent years, binary translation has been used in various other settings. Intel's IA-32 EL framework provides a software layer to allow running 32-bit x86 applications on IA-64 machines without any hardware support. Qemu [17] uses binary translation to emulate multiple source-destination architecture pairs. Qemu avoids dealing with the complexity of different instruction sets by encoding each instruction as a series of operations in C. This allows Qemu to support many source-destination pairs at the cost of performance (typically 5-10x slowdown). Transmeta Crusoe [12] uses on-chip hardware to translate x86 CISC instructions to RISC operations on-the-fly. This allows them to achieve comparable performance to Intel chips at lower power consumption. Dynamo and Dynamo-RIO [3,6] use dynamic binary translation and optimization to provide security guarantees, perform runtime optimizations and extract program trace information. Strata [19] provides a software dynamic translation infrastructure to implement runtime monitoring and safety checking.
We have found that this approach of first learning several peephole translations in an offline phase and then applying them to simultaneously perform register mapping and instruction selection produces an efficient code generator. In future, we wish to apply this technique to other applications of code generation, such as just-in-time compilation and machine virtualization.