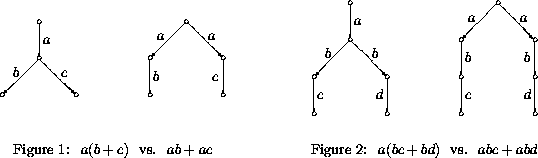
When comparing models or equivalences for concurrent systems, it is common practice to distinguish between linear time and branching time semantics (see for instance DE BAKKER, BERGSTRA, KLOP & MEYER [1] or PNUELI [9]). In the former, a process is completely determined by the observable content of its possible (partial) runs, whereas in the latter also the information is preserved where two different courses of action diverge (although branching of identical courses of action may still be neglected). Standard examples are the processes in Figure 1 and 2.
In Figure 1, both processes have two complete runs, whose observable
content is ab and ac respectively. However, in 
these runs
diverge after the a-step, whereas in ab+ac they diverge at the
onset. This difference can also be described by pointing out that
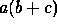has a partial run with observable content a that is an
initial part of each of the runs ab and ac, whereas 
has no
such run. Hence the two processes are linear time equivalent, but
not branching time equivalent. Similarly, the two processes of Figure
2 are identified in linear time semantics but not in branching
time semantics, since only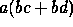 
has a run a that is an initial
part of both of the runs abc and abd.
Figure 3 illustrates that in branching time semantics only the
branching of different courses of action is of importance.
The processes 
and ab+ab are bisimulation equivalent
[8], which is widely considered to be the prime example of
a branching time equivalence. Nevertheless, the two runs with observable
content ab diverge at a different state. One
could employ a stricter
notion of branching time, in which also the branching of identical
courses of action would be taken into account. Under such a notion, the
processes of Figure 3 should be distinguished, but the ones of
Figure 4 could safely be identified.
It should be pointed out that branching time is not the definition of a particular model or semantic equivalence, but a criterion that can be satisfied by models or equivalences. A model or equivalence that satisfies this criterion is said to be a branching time model or equivalence, to respect branching time, or to respect the branching structure of processes. Call two processes, represented as labelled transition systems, tree equivalent if their unfoldings into trees are isomorphic. The two processes of Figure 4 for instance are tree equivalent, whereas the ones of Figure 1-3 are not. Tree equivalence is strictly finer than bisimulation equivalence and thus certainly preserves the information on where different courses of action diverge. Hence it constitutes a second example of a branching time equivalence. Moreover, unlike bisimulation equivalence, it would still be a branching time equivalence under the stricter interpretation of branching time contemplated above.
For processes without silent moves, it is commonly agreed that an
equivalence respects branching time iff it is finer than or equal to
bisimulation equivalence. Hence this yield a candidate for a
formal definition of the concept of a branching time equivalence.
However, in the presence of silent moves, or 
-steps, the
situation is less clear. In VAN GLABBEEK & WEIJLAND [7]
it is argued that branching bisimulation, that in the absence of
silent moves coincides with plain bisimulation, takes over this rôle
of bisimulation in the presence of 
's. However, this is not
inherent in the definition of the equivalence, and was meant to be a
result rather than a definition. The reasoning of [7] is
illustrated in Figures 5 and 6.
The first process in Figure 5 has a run with observable content ab, that diverges from the run with observable content ac at the same point where it diverges from the run ad. Thus it does not pass through a state in which it is still possible to continue with a course of action that involves a c, but not possible to continue with a course of action involving a d. Such a run is not present in the other process. It follows that these processes have a different branching structure and can not be identified by a branching time equivalence. As MILNER's notion of weak bisimulation [8] identifies both processes, it does not respect branching time. The notion of branching bisimulation on the other hand gives rise to a finer equivalence that does distinguish the processes of Figure 5. The processes of Figure 6 are branching bisimulation equivalent however, and indeed no argument can be construed that would indicate disrespect of branching time, the key argument being that the various runs with observable content ab can be regarded as the same course of action.
The best definition of a branching time equivalence so far is perhaps
the one implicit in the notion of a consistent colouring,
introduced in [7]: An equivalence respects branching
time if the colouring on processes/states, obtained by giving
equivalent processes the same colour, is consistent in the sense
of [7]. Here a sequence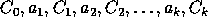 
is a concrete coloured trace of a process
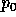if there is a run 
, such that process 
has colour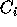 
;
a coloured trace of p is a sequence 
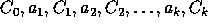obtained from a concrete coloured trace of p by
replacing any subsequence 
by C;
and a colouring is consistent if processes with the
same colour have the same set of coloured traces. The idea behind a
consistent colouring is that processes with the same colour have the
same potential of further courses of action. A coloured trace
indicates how these potentials vary (diminish) during a run.
As expected, under this definition branching bisimulation turns out to
be the coarsest branching time equivalence.
Although this definition captures the concept of branching time
reasonably well, it has the disadvantage of being tailored to a
setting with silent moves (through the reduction
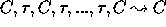). What would be more convincing
would be a definition that in no way refers to internal actions, and
still yields branching bisimulation as the coarsest equivalence
respecting the branching structure of processes. Moreover, it would be
nice to know what precisely the branching structure of a process is.
This is the goal of the present paper. I will formally define the
branching structure of a process, and declare an equivalence to
respect branching time iff it only relates processes with the same
branching structure. This will be the case iff the equivalence is
finer than or equal to branching bisimulation equivalence. Similarly a
model of concurrency respects branching time iff processes that are
represented by the same semantic object have the same branching
structure.
