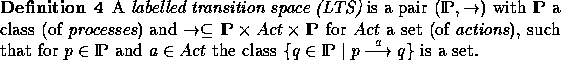
In this section I will instantiate the general definition of branching time from the previous section for equivalences on models of concurrency that can be regarded as labelled transition spaces.
Notation: Write 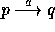 for
for 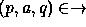 and
and 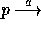 for
for 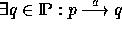 .
.
The elements of 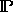 represent the processes we are interested in,
and
represent the processes we are interested in,
and 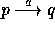 means that process p can evolve into process q
while performing the action a. I use the word `space' instead
of `system' to emphasize that the elements of an LTS are all
systems under investigation, and not merely the states of a single
system.
means that process p can evolve into process q
while performing the action a. I use the word `space' instead
of `system' to emphasize that the elements of an LTS are all
systems under investigation, and not merely the states of a single
system.
It remains to determine the observable content of a run.
In case all actions are observable, let
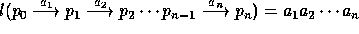 . In case
. In case 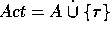 , where
, where  denotes an internal or unobservable
action, the observable content
denotes an internal or unobservable
action, the observable content 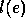 of a run e is the same
sequence, but from which all
of a run e is the same
sequence, but from which all  's are removed. This completes the
definition of the branching structure of members of an LTS.
's are removed. This completes the
definition of the branching structure of members of an LTS.
In [5] is has been established that weak back and forth bisimulation equivalence coincides with branching bisimulation equivalence. Hence is follows that
If in Definition 3 the coarsest congruence would be replaced by the coarsest weak congruence, the resulting `branching structure' would have a distinct linear time flavour, as it would be nothing more than the so-called trace set of a process. The coarsest strong congruence on the other hand would on an LTS be the identity relation, causing the branching structure to become the strict branching structure. On an LTS two processes have the same strict branching structure iff they are tree equivalent, as follows immediately from the definitions. Silent actions play no special rôle here.