

Next: What is nice
Up: What is branching time
Previous: The case of
Term models, in which a process is represented as an expression in a
system description language, labelled event structures, Petri nets,
process graphs, and many other models of concurrency can be regarded
as labelled transition spaces. Namely, there are canonical definitions
of the transition relations 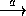 between two terms, event
structures, nets, etc. For these models the definitions of runs and
their visible content from the previous section apply, and hence it
is determined what it means for a semantic equivalence on such a model
to respect branching time. Unless causality is taken to be part of the
observable content of runs, in which case
between two terms, event
structures, nets, etc. For these models the definitions of runs and
their visible content from the previous section apply, and hence it
is determined what it means for a semantic equivalence on such a model
to respect branching time. Unless causality is taken to be part of the
observable content of runs, in which case 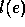 could be modelled as
a mixed ordering (cf. DEGANO, DE NICOLA & MONTANARI
[4]) and the coarsest branching time equivalence would be
history preserving branching bisimulation equivalence.
could be modelled as
a mixed ordering (cf. DEGANO, DE NICOLA & MONTANARI
[4]) and the coarsest branching time equivalence would be
history preserving branching bisimulation equivalence.
Some models however, such as the failures model of BROOKES, HOARE & ROSCOE [3], can not be regarded as labelled
transition spaces. In these cases it is often difficult to associate
with a process a prefix-ordered set of runs. However, usually such a
model can be canonically interpreted as the homomorphic image of a
labelled transition space. In that case the model can be said to
respect branching time iff the canonical homomorphism does not map two
processes which have a different branching structure to the same
element. Similarly, an equivalence on such a model respects branching
time iff no two images of processes with a different branching
structure are equivalent.


Next: What is nice
Up: What is branching time
Previous: The case of
Rob van Glabbeek
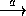 between two terms, event
structures, nets, etc. For these models the definitions of runs and
their visible content from the previous section apply, and hence it
is determined what it means for a semantic equivalence on such a model
to respect branching time. Unless causality is taken to be part of the
observable content of runs, in which case
between two terms, event
structures, nets, etc. For these models the definitions of runs and
their visible content from the previous section apply, and hence it
is determined what it means for a semantic equivalence on such a model
to respect branching time. Unless causality is taken to be part of the
observable content of runs, in which case 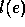 could be modelled as
a mixed ordering (cf. DEGANO, DE NICOLA & MONTANARI
[4]) and the coarsest branching time equivalence would be
history preserving branching bisimulation equivalence.
could be modelled as
a mixed ordering (cf. DEGANO, DE NICOLA & MONTANARI
[4]) and the coarsest branching time equivalence would be
history preserving branching bisimulation equivalence.